The Grammar of Graphics: notes on first reading

Leland Wilkinson’s The Grammar of Graphics is a classic in the data visualization literature. Wilkinson created a framework that coherently ties together many aspects of designing, implementing, reading, and understanding a graphic. It’s a useful approach and has been fairly influential: The popular R package ggplot2 is, more or less, an implementation of Wilkinson’s ideas, and I also see their influence in the software Tableau (about which more another time). Wilkinson himself helped to build these ideas into SPSS’s Graphics Production Language (GPL) and then SPSS Visualization Designer.

So what’s so special here? One of the core ideas is to start with the raw data and think about all the transformations, summaries, etc. that go into graphing it. With a good framework, this can help us see connections between different graphs and create new ones. (The opposite extreme is a “typology” or list of graph types, like you get in Excel: do you want a bar chart, a pie chart, a line chart, or one of these other 10 types? Such a list has no deep structure.) Following Wilkinson’s approach, you’ll realize that a pie chart is basically just a stacked bar chart plotted in polar coordinates, with bar height mapped to pie-slice angle… and that can get you thinking: What if I mapped bar height to radius, not angle? What if I added a variable and moved to spherical coordinates? What if I put a scatterplot in polar coordinates too? These may turn out to be bad ideas, but at least you’re thinking — in a way that is not encouraged by Excel’s list of 10 graph types.

But, of course, thinking is hard, and so is this book. Reading The Grammar of Graphics requires much more of a dedicated slog than, say, Edward Tufte’s books, which you can just flip through randomly for inspiration and bite-sized nuggets of wisdom. (I admire Tufte too, but I have to admit that Wilkinson’s occasional jabs at Tufte were spot-on and amused me to no end.) It’s a book full of wit and great ideas, but also full of drawn-out sections that require serious focus, and it takes a while to digest it all and put it together in your mind.

So, although I’d highly recommend this book to anyone deeply interested in visualization, I’m still digesting it. What follows is not a review but just notes-to-self from my first read-through: things to follow up on and for my own reference. It might not be particularly thrilling for other readers.

(Bold indicates things I meant to follow up. Also, the page numbers refer to the 1st edition, from 1999. After I finished reading, I learned there was a 2nd edition in 2005; I’m not sure what is new there.)

• p. ix: what are his collaborators Dan Rope and Dan Carr doing now? Dan Carr is at George Mason University and still works on visualization, but I’m curious about Rope. Edit: Noah Iliinsky left a comment to say Dan Rope is at IBM working on SPSS.
• p. 2: summary of his reasons for wanting to get at structure, not just a typology of graphs
• p. 14: he says his system allows for dynamic, exploratory graphics — but it turns out he doesn’t follow this idea much in this book. They are all static, unless you count the in-progress “graphboard” in Chapter 13. Perhaps he covers dynamic graphics in the 2nd edition?
• p. 15: “This system is capable of producing some hideous graphics. … This system cannot produce a meaningless graphic, however.” In other words, the framework doesn’t make your graphs pretty; but it does ensure they say only what’s really in the data, not something you made up.
• p. 15: “I also cannot disagree strongly enough with statements about the dangers of putting powerful tools in the hands of novices. … The obvious problems caused by this situation do not justify blunting our tools, however. They require better education in the imaginative and disciplined use of these tools.” Amen.
• p. 17: “statistical graphics are often most effective when they exploit mental models that evolved as humans struggled to survive in a competitive world…” References to look up:
  • Pinker, S. (1990). A theory of graph comprehension. In R. Friedle (Ed.), Artificial intelligence  and the future of testing. Hillsdale, NJ: Erlbaum, pp. 73-126.
  • Symanzik et al. (1997). Dynamic statistical graphics in the C2 virtual environment. Computing Science and Statistics, 29(2), 35-40.
• p. 18: references on history of statistical graphics: Collins 1993, Funkhouser 1937, Tilling 1975, Beniger & Robyn 1978, Fienberg 1979, Robinson 1982, Stigler 1983, Tufte 1983/1990/1997, Wainer 1997 … and on theory of statistical graphics: Bertin 1967/1977, Cleveland 1985, Pinker 1990, Brodlie 1993, MacEachren 1995, Roth et al. 1995
• p. 46: “scientists like Skinner (1969) have argued that behavioral data are best understood by avoiding unobservables and inferences. Skinner even rejected statistical modeling, arguing that smoothing or aggregation obscures details that could help falsify theories.” An interesting point, though taken to the extreme — Wilkinson gives a good counterexample.
• p. 56: GQL “functions like SQL but operates on graphical objects rather than relational variables” ??? Papantonakis and King 1995
• p. 57: “in a landmark book, now out of print and seldom read by statisticians, Coombs (1964) … believed that the prevalent practice of modeling based on cases-by-variables data layouts often prevents researchers from considering more parsimonious structural theories and keeps them from noticing meaningful patterns in their data.” Too bad it’s hard to find a copy: C.H. Coombs, 1964, A Theory of Data, Wiley. Edit: see my notes on Coombs’ book.
• p. 60, 229: probability plots and probability scales — is this a generalization of Q-Q plots?
• p. 109, 119: when assigning variables to dimensions, think about “integral” vs “separable” dimensions: it’s easy to read size as one variable and texture as another (they’re separable), but it can be difficult to read a graphic where hue depicts one variable and brightness depicts another (they are integral). “Kosslyn (1994) offers useful guidelines.”
• p. 115: “there may be good reasons to dislike chartjunk, and Tufte’s graphics are indisputably beautiful, but the crusade against chartjunk is not supported by scientific research and psychological theory.”
• p. 116: regarding Chernoff faces, “Tufte advised that symmetries should be avoided in statistical graphics because they introduce unnecessary redundancies. … it makes little sense to enlist a wired-in perceptual mechanism and then defeat it by radical surgery.”
• p. 128, 132: “MacEachren (1992) recommends saturation for representing uncertainty in a graphic.” Good advice right now as I’m looking into intuitive ways to convey uncertainty and measures of error. MacEachren also seems to have a 2005 paper focused on this issue with geospatial data in particular. MacEachren also suggests using blur; see also Wilkinson’s “fuzzygrams” in Fig 2.4b on p.23 (10th page of the PDF) of this paper.
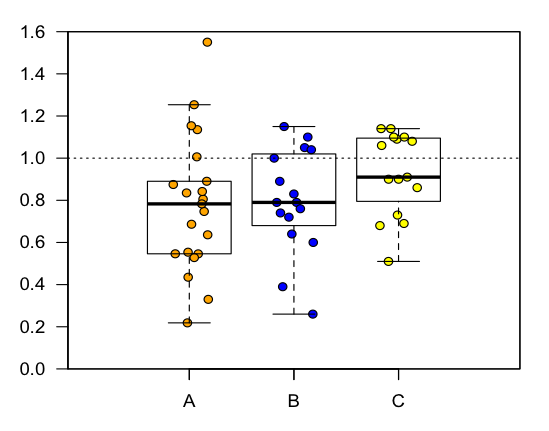
• p. 138: I really like the “dot-box plot” here: box plots overlaid with stacked dots of the actual observations, so you can see both the raw data and the box-plot summary. Here is an example in R although with jittering, not stacking. (Rafe Donahue’s excellent notes are also full of great advice on including raw data, not just statistical summaries, in your graphics.)

• p. 149: use of mini thermometer glyphs, called “therms”: I don’t like his example, but I can imagine using these overlaid on a map of US states to show which states’ values of a variable are above or below the average; and varying the width of the therms by the sample size, or inverse CV, or some other measure of precision — we’re more confident about the fatter thermometers, whatever their reading is. Ah — it turns out there’s an example of this on the last page of Dunn 1987.
• p. 179: nice example of using a “modal smoother” — instead of finding the local mean, it finds the local mode, which can help to highlight discontinuities in the data that would otherwise be smoothed together. This seems to be section 8.3.2 in Scott 1992 (Amazon; PDF without the figures).
• p. 206: “What our general design attempts to do is to get away from static graphic entities and instead to treat graphs and their statistical methods like little creatures that respond to different messages and do their calculations in their own peculiar ways. … Some contemporary graphics and statistics programs can perform part of this scenario already because they are hard-wired to animate, link, drill-down, and brush within certain widely-used graphics such as bar charts and scatterplots. The real trick, however, is to replicate this behavior for any graph, on any scale, in any coordinate system, in any ensemble of graphics. A graphics grammar gives us the means.”
• p. 207: nice table illustrating statistical summaries in 1, 2, and 3D
• p. 214: “the common prescription … that bars require a zero base to be meaningful … [is a statement] about scales rather than graphics.” Bars show an interval, giving us the bottom value and the top value. Error bars are bars too, and there we’re interested in the interval as a whole; no sense in fixing one end at 0. But fixing one end of all the bars at zero allows you to compare ratios, if that’s your data summary of interest. If you expect readers will care about ratios, show them 0 on the graph, no matter whether you’re using bars or points or whatever to display the data.
• p. 214: he explains the distinction between a transformation on variables, vs on scales, vs on coordinates (which I still need to clarify in my head and illustrate with a plot)
• p. 241: interesting explanation of pivoting a table, comparing log-linear models vs logistic regression models
• p. 250-251: often we do a variable transformation so the model assumptions are met, but we actually care about interpreting the results in terms of the original (untransformed) variables; here’s a great example of using a projection to show the results of transforming variables for a WLS regression
• p. 297-298: often parallel coordinates plots (whether rectangular or polar) just look like a mess, so I rarely think to use them. But here’s an example where the data really do cluster meaningfully and the plot could be useful indeed.
• p. 267: I need to re-read this: he overlaid the scatterplot with contours of some other variable? i.e. the contours do not show density of the scatterplot points, but a 3rd variable? This may be a useful trick.
• p. 270-271: the range of your graphics should be the range of the data, even if you’re focused on plotting a summary statistic which is much less variable than the raw data. Clipping to conserve white space “is a form of lying with graphics”; “Graphics programs that encourage them to do this thoughtlessly are promoting scientific malpractice.”
• p. 274: nifty idea to show “isochrones (contours of equal travel time)” or to warp your map projection so that distance on the page is approximately proportional to travel time, not to actual geographic distance.
• p. 277: read Pinker 1997 to understand how our brain’s visual system understands projections
• p. 280: read up on shingling and the trellis display: Cleveland 1993; Becker, Cleveland, and Shyu 1996
• p. 292: “Unfortunately, rectangular bins do not represent equal sampling areas on the surface of a sphere” — hexagonal tiles are better? see Carr et al. 1992
• p. 318-319: scatterplot matrices (SPLOMs) can be useful — I like his idea of using color within each cell to separate out observations by a categorical variable, including overlaying separate kernel density estimates for each category (instead of one histogram for all categories) … I should add an image of this
• p. 320: the “mobile” representing a regression tree is an interesting idea
• p. 330:  “Labeling of graphic elements is sometimes preferable to axes or separate legends because it allows local look-up without changing our focus and it can provide exact values without requiring comparative judgments.” …as I pointed out in a recent post.
• p. 333: he really doesn’t like scale breaks (where the axis has a zigzag or double line to indicate that you’re not showing part of that variable’s range, i.e. so you can show 0 at one end but allow the actual range of the data to take up most of the graph). If you want zero on the graph, you need to include the whole range in between, or else you’re misleading the reader.
• p. 339-340: I really like his graphboard idea (which Tableau seems to have borrowed? stolen?) — especially this aspect: “I have made efforts throughout the design of this interface to eliminate dialogs, wizards, and other order-dependent devices so that both novices and experts can explore, backtrack, and modify without being forced through steps someone else imagined to be helpful.” … “all actions in the graphboard are reversible, so it is straightforward to return to where one was several steps back. There is no need for UNDO.”
• p. 356: “a propositional system developed by mathematical logicians … and implemented by cognitive psychologists (see Rumelhart, 1977; Anderson, 1983) that influenced the development of object-oriented design itself.” That sounds like quite a trip for these ideas — I wonder about the story there.
• p. 371: “The subtleties of this graphic (including Minard’s errors and omissions) are revealed through a detailed analysis of the data in light of the specification. Constructing a valid specification forces us to reconstruct the data properly.” Section 15.1 is a great read, where Wilkinson wonderfully picks apart Minard’s famous map of Napoleon’s march on Russia (as well as Tufte’s commentary on Minard). Minard’s original is, of course, more beautiful than Wilkinson’s reconstruction, but it contains a few “ungrammatical” mistakes that become obvious only when you try to reconstruct it; and it turns out to contain even more dimensions of data than Tufte realized or credited it with. Wilkinson also adds yet another dimension, using dash lengths to count off the days and hence to highlight the pace of the armies’ retreat. Apparently there are also a few other Minard-like maps in Koester 1982 and Barraclough 1984

Finally, some cute moments of humor (rather than statistical/visual insight):

• p. 129: orientation comes from orient, sunrise, in the East; the converse is occident, sunset, in the West… so perhaps a disoriented alignment should be called occidentation? 😛
• p. 129: Besag 1986 has “my favorite title for a statistical paper on this or any subject” … that title being “On the Statistical Analysis of Dirty Pictures”
• p. 131: “Some countries have laws against this sort of thing; check with your local authorities before using flags in graphics.”
• p. 133: “a book is not the ideal format for presenting animation. For a glimpse, flip the pages and watch the page numbers in the corner change.”
• p. 193: “Our fiddler crabs have installed a convex hull to establish a gated retirement community.”
• p. 196: “The results of this analysis have absolutely no commercial potential.”

That’s plenty for now. Soon I intend to add some notes from reading Hadley Wickham’s ggplot2 book, which gives R users access to many of these ideas.