Hypothesis tests will not answer your question

Assume your hypothesis test concerns whether a certain effect or parameter is 0. With interval estimation, you can distinguish several options:

1. The effect is precisely-measured and the interval includes 0, so we can ignore it.
2. The effect is precisely-measured but the interval doesn’t include 0, but it’s close enough to be negligible for practical purposes, so we can ignore it.
3. The effect is precisely-measured to be far from 0, so we can keep it as is.
4. The effect is poorly-measured but we’re confident it’s not 0, so we can keep it but should still get more data to raise precision.
5. The effect is poorly-measured and might be 0, so we definitely need more data before deciding what to do.

…as illustrated below:

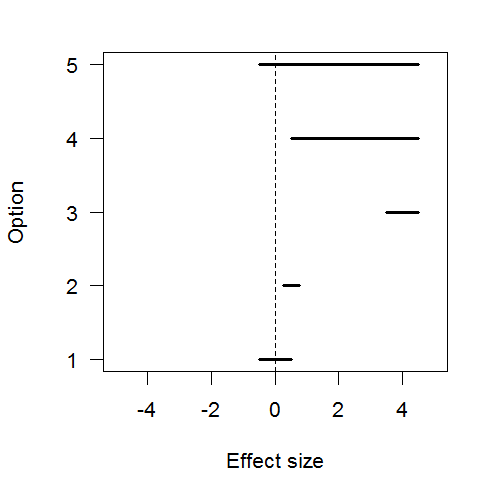
Imagine you’re a scientist, making inferences about how the world works; or an engineer, building a tool that relies on knowing the size of these effects. You would like to distinguish between (1&2) vs. (3) vs. (4&5). Journal readers would like you to publish results for cases (1&2) or (3), and should want you to collect more data before publishing in cases (4&5).

Instead, hypothesis testing conflates (1&5) vs. (2&3&4). That doesn’t help you much!

In particular, when you conflate (1&5) it makes for bad science, as people in practice tend to interpret “not statistically significant” as “the effect must be spurious.” Instead they should interpret it as “either the effect is spurious, or it might be practically significant but not measured well enough to know.” And even if you were aware of this, and if you did collect more data to get out of situations (1&5), a hypothesis test still wouldn’t help you distinguish (2) vs. (3) vs. (4).

Finally, this is an issue whether your hypothesis tests are Frequentist or Bayesian. As John Kruschke’s excellent book on Doing Bayesian Data Analysis points out, if you do a Bayesian model comparison of one model with a spiked prior at and another with some diffuse prior for , “all that this model comparison tells us is which of two unbelievable models is less unbelievable. [And] that is not all we want to know, because usually we also want to know what [parameter] values are credible” (p.427).

This is in addition to all the other problems with hypothesis tests. See my notes from reading Michael Oakes’ Statistical Inference for several more.

Sure, traditional hypothesis testing does have its uses, but they are rather limited. I find that interval estimation does a better job of supporting careful thought about your analysis.