Small Area Estimation is a field of statistics that seeks to improve the precision of your estimates when standard methods are not enough.
Say your organization has taken a large national survey of people’s income, and you are happy with the precision of the national estimate: The estimated national average income has a tight confidence interval around it. But then you try to use this data to estimate regional (state, county, province, etc.) average incomes, and some of the estimates are not as precise as you’d like: their standard errors are too high and the confidence intervals are too wide to be useful.
Unlike usual survey-sampling methods that treat each region’s data independently, a Small Area Estimation model makes some assumptions that let areas “borrow strength” from each other. This can lead to more precise and more stable estimates for the various regions (if the assumptions are reasonable).
Also note that it is sometimes called Small Domain Estimation because the “areas” do not have to be geographic: they can be other sub-domains of the data, such as finely cross-classified demographic categories of race by age by sex.
If you are interested in learning about the statistical techniques involved in Small Area Estimation, it can be difficult to get started. This field does not have as many textbooks yet as many other statistical topics do, and there are a few competing philosophies whose proponents do not cross-pollinate so much. (For example, the U.S. Census Bureau and the World Bank both use model-based small area estimation but in quite different ways.)
Recently I gave a couple of short tutorials on getting started with SAE, and I’m polishing those slides into something stand-alone I can post. [Edit: I still haven’t polished them, but I’ve posted my old slides and code.] Meanwhile, below is a list of resources I recommend if you would like to be more knowledgeable about this field.
Textbooks on SAE:
- Nicholas Longford, Missing Data and Small-Area Estimation: Modern Analytical Equipment for the Survey Statistician, Springer, 2005. [Amazon]
- J.N.K. Rao, Small Area Estimation, Wiley-Interscience, 2003. [Amazon]; there also seems to be a 2nd edition on the way?
- Parimal Mukhopadhyay, Small Area Estimation in Survey Sampling, Narosa Publishing House, 1998. [Amazon]
- Platek, Rao, Särndal, and Singh (ed.), Small Area Statistics: An International Symposium, Wiley, 1987. [Amazon]
Book sections on SAE:
- Benjamin Kedem et al., Statistical Data Fusion, World Scientific, 2017. [Amazon]
- Wayne Fuller, Sampling Statistics, Wiley, 2009. Ch. 5.5, “Small area estimation,” pp. 311-324. [Amazon]
- Peter Congdon, Applied Bayesian Modelling, Wiley, 2003. Ch. 4.6, “Small domain estimation,” pp. 163-167. [Amazon has 2nd edition; SAE section number may be different.]
- Peter Congdon, Bayesian Statistical Modelling, Wiley, 2001. Ch. 8.8, “Small area and survey domain estimation,” pp. 415-421. [Amazon has 2nd edition; SAE section number may be different.]
Classic articles:
- Bradley Efron and Carl Morris, “Data Analysis Using Stein’s Estimator and Its Generalizations,” JASA, vol. 70, no. 350, pp. 311-319, 1975. [JSTOR]
Early popularization of shrinkage methods, from the Empirical Bayes point of view. - Robert Fay and Roger Herriot, “Estimates of Income for Small Places: An Application of James-Stein Procedures to Census Data,” JASA, vol. 74, no. 366, pp. 269-277, 1979. [JSTOR]
The classic area-level model (for survey data that’s already been aggregated to the level at which you want to publish estimates). - George Battese, Rachel Harter, and Wayne Fuller, “An Error-Components Model for Prediction of County Crop Areas Using Survey and Satellite Data,” JASA, vol. 83, no. 401, pp. 28-36, 1988. [JSTOR]
The classic unit-level model (for working with disaggregated data). - Chris Elbers, Jean Lanjouw, and Peter Lanjouw, “Micro–Level Estimation of Poverty and Inequality,” Econometrica, vol. 71, no. 1, pp. 355-364, 2003. [JSTOR]
Underlies the PovMap software that is made available by the World Bank and consequently in wide use.
Review articles:
- Gauri S. Datta, “Model-based approach to small area estimation,” pp. 251-288, Handbook of Statistics: Sample Surveys: Inference and Analysis, vol. 29B, eds.: D. Pfeffermann and C.R. Rao, North-Holland, 2009.
- Risto Lehtonen and Ari Veijanen, “Design-based methods of estimation for domains and small areas,” pp. 219-249, Handbook of Statistics: Sample Surveys: Inference and Analysis, vol. 29B, eds.: D. Pfeffermann and C.R. Rao, North-Holland, 2009.
- M. Ghosh and J. N. K. Rao, “Small area estimation: an appraisal,” Statist. Sci., vol. 9, no. 1, pp. 55 – 76, 1994. (See also comments and rejoinder.) [Project Euclid]
Other resources:
- Pushpal Mukhopadhyay and Allen McDowell, “Small Area Estimation for Survey Data Analysis using SAS Software,” SAS Global Forum 2011. [SAS]
Examples of unit-level and area-level estimation with PROC MIXED and hierarchical Bayes estimation with PROC MCMC. - Virgilio Gómez-Rubio, “Tutorial on Small Area Estimation,” 2008 useR! Conference. [Website]
Slides and R code from tutorial session. - Arman Bidarbakht-Nia et al., “Workshop on Concepts & Methods for Producing Disaggregated Statistics Using Census Data,” Bangkok, 2011. [Website]
Slides from tutorial session by UN-ESCAP staff. - World Bank staff et al. (?), “More Frequent, More Timely & More Comparable Data for Better Results,” PREM 2011. [Website]
Slides from workshop on poverty monitoring. - Bedi, Coudouel, and Simler (ed.), More Than a Pretty Picture: Using Poverty Maps to Design Better Policies and Interventions, The World Bank, 2007. [Amazon]
- Elliott, Cuzick, English, and Stern (ed.), Geographical and Environmental Epidemiology: Methods for Small-Area Studies, Oxford University Press, 1992. [Amazon]

Great resources! Looking forward to the longer treatment! I don’t do much survey research, but I have definitely done hierarchical modeling. I typically use mixed-effects/Bayesian approaches ala Gelman to “partially pool” subsets of the data towards the global trend. Are the SAE approaches you describe substantially different? How so?
Thanks, Harlan! Yep, many of the SAE approaches are mixed-effects models as you describe, but with a special focus on accounting for the survey weights and sampling variances explicitly. , where i indexes the small areas, and the observed
, where i indexes the small areas, and the observed 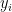 are already aggregated to the area level using sampling weights. So we usually also have a survey-design-based estimate of the area-level sampling variance
are already aggregated to the area level using sampling weights. So we usually also have a survey-design-based estimate of the area-level sampling variance 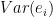 that we often just treat as known. Then it’s just a matter of estimating the area-level random-effect variance
that we often just treat as known. Then it’s just a matter of estimating the area-level random-effect variance 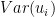 and regression coefficients
and regression coefficients 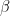 , then combining it all to get estimates of
, then combining it all to get estimates of 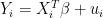 .
.
In the examples I’ll post, you’ll see a model like
More details to follow!