surveyCV: K-fold cross validation for complex sample survey designs

I’m fortunate to be able to report the publication of a paper and associated R package co-authored with two of my undergraduate students (now alums), Cole Guerin and Thomas McMahon: “K-Fold Cross-Validation for Complex Sample Surveys” (2022), Stat, doi:10.1002/sta4.454 and the surveyCV R package (CRAN, GitHub).

The paper’s abstract:

Although K-fold cross-validation (CV) is widely used for model evaluation and selection, there has been limited understanding of how to perform CV for non-iid data, including from sampling designs with unequal selection probabilities. We introduce CV methodology that is appropriate for design-based inference from complex survey sampling designs. For such data, we claim that we will tend to make better inferences when we choose the folds and compute the test errors in ways that account for the survey design features such as stratification and clustering. Our mathematical arguments are supported with simulations and our methods are illustrated on real survey data.

Long story short, traditional K-fold CV assumes that your rows of data are exchangeable, such as iid draws or simple random samples (SRS). But in survey sampling, we often use non-exchangeable sampling designs such as stratified sampling and/or cluster sampling.1

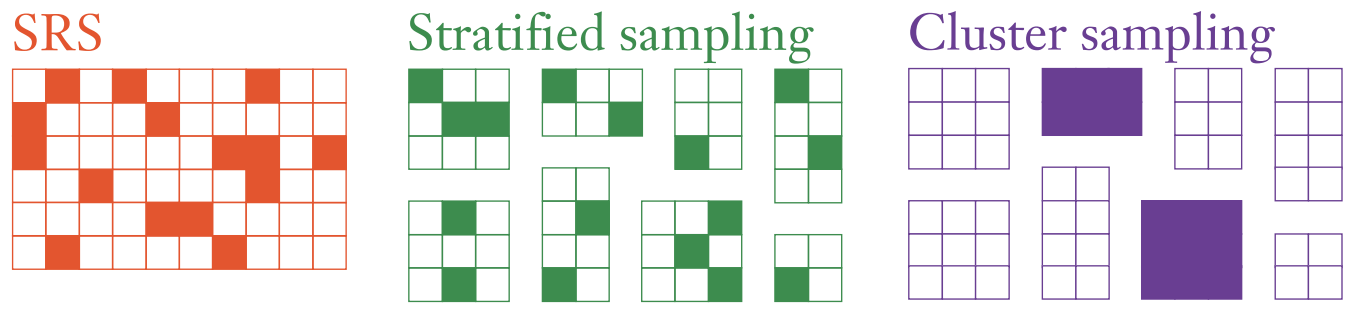
Illustration of simple random sampling, stratified sampling, and cluster sampling

Our paper explains why in such situations it can be important to carry out CV that mimics the sampling design.2 First, if you create CV folds that follow the same sampling process, then you’ll be more honest with yourself about how much precision there is in the data. Next, if on these folds you train fitted models and calculate test errors in ways that account for the sampling design (including sampling weights3), then you’ll generalize from the sample to the population more appropriately.

If you’d like to try this yourself, please consider using our R package surveyCV. For linear or logistic regression models, our function cv.svy() will carry out the whole K-fold Survey CV process:

  • generate folds that respect the sampling design,
  • train models that account for the sampling design, and
  • calculate test error estimates and their SE estimates that also account for the sampling design.

For more general models, our function folds.svy() will partition your dataset into K folds that respect any stratification and clustering in the sampling design. Then you can use these folds in your own custom CV loop. In our package README and the intro vignette, we illustrate how to use such folds to choose a tuning parameter for a design-consistent random forest from the rpms R package.

Finally, if you are already working with the survey R package and have created a svydesign object or a svyglm object, we have convenient wrapper functions folds.svydesign(), cv.svydesign(), and cv.svyglm() which can extract the relevant sampling design info out of these objects for you.

It was very rewarding to work with Cole and Thomas on this project. They did a lot of the heavy lifting on setting up the initial package, developing the functions, and carrying out simulations to check whether our proposed methods work the way we expect. My hat is off to them for making the paper and R package possible.

Some next steps in this work:

  • Find additional example datasets and give more detailed guidance around when there’s likely to be a substantial difference between usual CV and Survey CV.
  • Build in support for automated CV on other GLMs from the survey package beyond the linear and logistic models. Also, write more examples of how to use our R package with existing ML modeling packages that work with survey data, like those mentioned in Section 5 of Dagdoug, Goga, and Haziza (2021).
  • Try to integrate our R package better with existing general-purpose R packages for survey data like srvyr and for modeling like tidymodels, as suggested in this GitHub issue thread.
  • Work on better standard error estimates for the mean CV loss with Survey CV. For now we are taking the loss for each test case (e.g., the squared difference between prediction and true test-set value, in the case of linear regression) and using the survey package to get design-consistent estimates of the mean and SE of this across all the test cases together. This is a reasonable survey analogue to the standard practice for regular CV—but alas, that standard practice isn’t very good. Bengio and Grandvalet (2004) showed how hard it is to estimate SE well even for iid CV. Bates, Hastie, and Tibshirani (2021) have recently proposed another way to approach it for iid CV, but this has not been done for Survey CV yet.
  1. For instance, stratified sampling can be more statistically efficient than a SRS: by drawing random samples within each of several strata independently, you can reduce the variability of your estimators, leading to narrower confidence intervals etc. On the other hand, cluster sampling can be less statistically efficient but more cost-effective: it may cost too much to send a face-to-face survey interviewer to a SRS of households across the entire USA because they would be so widely dispersed, so instead you might take a sample of towns/cities (clusters) and then sample households within those selected clusters.
  2. A common misconception is that each fold should mimic the full dataset as much as possible, so sometimes people stratify their CV folds on variables that weren’t used to stratify the original sampling design. But we claim that this underestimates variability in the sampling process, making CV overconfidently choose models that are larger than you can realistically afford to fit. Instead, each fold should mimic the way the full dataset was sampled.
  3. Note that sampling weights are distinct from other kinds of statistical weights.