Small Area Estimation is a field of statistics that seeks to improve the precision of your estimates when standard methods are not enough.
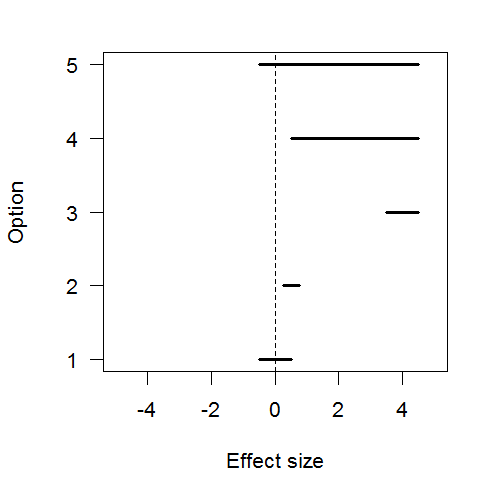
Say your organization has taken a large national survey of people’s income, and you are happy with the precision of the national estimate: The estimated national average income has a tight confidence interval around it. But then you try to use this data to estimate regional (state, county, province, etc.) average incomes, and some of the estimates are not as precise as you’d like: their standard errors are too high and the confidence intervals are too wide to be useful.
Unlike usual survey-sampling methods that treat each region’s data independently, a Small Area Estimation model makes some assumptions that let areas “borrow strength” from each other. This can lead to more precise and more stable estimates for the various regions (if the assumptions are reasonable).
Also note that it is sometimes called Small Domain Estimation because the “areas” do not have to be geographic: they can be other sub-domains of the data, such as finely cross-classified demographic categories of race by age by sex.
If you are interested in learning about the statistical techniques involved in Small Area Estimation, it can be difficult to get started. This field does not have as many textbooks yet as many other statistical topics do, and there are a few competing philosophies whose proponents do not cross-pollinate so much. (For example, the U.S. Census Bureau and the World Bank both use model-based small area estimation but in quite different ways.)
Recently I gave a couple of short tutorials on getting started with SAE, and I’m polishing those slides into something stand-alone I can post. [Edit: I still haven’t polished them, but I’ve posted my old slides and code.] Meanwhile, below is a list of resources I recommend if you would like to be more knowledgeable about this field. Continue reading “Small Area Estimation resources”